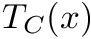Doxygen 1.9.1
Toolkit for Adaptive Stochastic Modeling and Non-Intrusive ApproximatioN: Tasmanian v8.2 (development)
Classes | Typedefs | Functions
Miscellaneous utility functions and aliases
Optimization
Collaboration diagram for Miscellaneous utility functions and aliases:

Classes

struct  TasOptimization::OptimizationStatus
 

Typedefs

using TasOptimization::ObjectiveFunctionSingle = std::function< double(const std::vector< double > &x)>
 Generic non-batched objective function signature. More...
 
using TasOptimization::ObjectiveFunction = std::function< void(const std::vector< double > &x_batch, std::vector< double > &fval_batch)>
 Generic batched objective function signature. More...
 
using TasOptimization::GradientFunctionSingle = std::function< void(const std::vector< double > &x_single, std::vector< double > &grad)>
 Generic non-batched gradient function signature. More...
 
using TasOptimization::ProjectionFunctionSingle = std::function< void(const std::vector< double > &x_single, std::vector< double > &proj)>
 Generic non-batched projection function signature. More...
 

Functions

void TasOptimization::checkVarSize (const std::string method_name, const std::string var_name, const int var_size, const int exp_size)
 
ObjectiveFunction TasOptimization::makeObjectiveFunction (const int num_dimensions, const ObjectiveFunctionSingle f_single)
 Creates a TasOptimization::ObjectiveFunction object from a TasOptimization::ObjectiveFunctionSingle object. More...
 
void TasOptimization::identity (const std::vector< double > &x, std::vector< double > &y)
 Generic identity projection function.
 
double TasOptimization::computeStationarityResidual (const std::vector< double > &x, const std::vector< double > &x0, const std::vector< double > &gx, const std::vector< double > &gx0, const double lambda)
 

Detailed Description

Several type aliases and utility functions similar to the he DREAM module.

Typedef Documentation

◆ ObjectiveFunctionSingle

using TasOptimization::ObjectiveFunctionSingle = typedef std::function<double(const std::vector<double> &x)>

Generic non-batched objective function signature.

Accepts a single input x and returns the value of the function at the point x.

Example of a 2D quadratic function:

ObjectiveFunctionSingle f = [](const std::vector<double> &x)->
double {
return x[0] * x[0] + 2.0 * x[1] * x[1];
};
TasOptimization::ObjectiveFunctionSingle
std::function< double(const std::vector< double > &x)> ObjectiveFunctionSingle
Generic non-batched objective function signature.
Definition: tsgOptimizationUtils.hpp:102

◆ ObjectiveFunction

using TasOptimization::ObjectiveFunction = typedef std::function<void(const std::vector<double> &x_batch, std::vector<double> &fval_batch)>

Generic batched objective function signature.

Batched version of TasOptimization::ObjectiveFunctionSingle. Accepts multiple points x_batch and writes their corresponding values into fval_batch. Each point is stored consecutively in x_batch so the total size of x_batch is num_dimensions times num_batch. The size of fval_batch is num_batch. The Tasmanian optimization methods will always provide correct sizes for the input, no error checking is needed.

Example of a 2D batch quadratic function:

ObjectiveFunction f = [](std::vector<double> const &x, std::vector<double> &y)->
void {
for(size_t i=0; i<y.size(); i++) {
y[i] = x[2*i] * x[2*i] + 2.0 * x[2*i+1] * x[2*i+1];
}
};
TasOptimization::ObjectiveFunction
std::function< void(const std::vector< double > &x_batch, std::vector< double > &fval_batch)> ObjectiveFunction
Generic batched objective function signature.
Definition: tsgOptimizationUtils.hpp:124

◆ GradientFunctionSingle

using TasOptimization::GradientFunctionSingle = typedef std::function<void(const std::vector<double> &x_single, std::vector<double> &grad)>

Generic non-batched gradient function signature.

Accepts a single input x_single and returns the gradient grad of x_single. Note that the gradient and x_single have the same size.

Example of a 2D batch quadratic function:

GradientFunctionSingle g = [](std::vector<double> const &x, std::vector<double> &grad)->
void {
grad[0] = 2.0 * x[0];
grad[1] = 4.0 * x[0];
};
TasOptimization::GradientFunctionSingle
std::function< void(const std::vector< double > &x_single, std::vector< double > &grad)> GradientFunctionSingle
Generic non-batched gradient function signature.
Definition: tsgOptimizationUtils.hpp:159

◆ ProjectionFunctionSingle

using TasOptimization::ProjectionFunctionSingle = typedef std::function<void(const std::vector<double> &x_single, std::vector<double> &proj)>

Generic non-batched projection function signature.

Accepts a single input x_single and returns the projection proj of x_single onto a user-specified domain.

Example of 2D projection on the box of [-1, 1]

ProjectionFunctionSingle p = [](std::vector<double> const &x, std::vector<double> &p)->
void {
p[0] = std::min(std::max(x[0], -1.0), 1.0);
p[1] = std::min(std::max(x[1], -1.0), 1.0);
};
TasOptimization::ProjectionFunctionSingle
std::function< void(const std::vector< double > &x_single, std::vector< double > &proj)> ProjectionFunctionSingle
Generic non-batched projection function signature.
Definition: tsgOptimizationUtils.hpp:175

Function Documentation

◆ checkVarSize()

void TasOptimization::checkVarSize ( const std::string  method_name,
const std::string  var_name,
const int  var_size,
const int  exp_size 
)
inline

Checks if a variable size var_name associated with var_name inside method_name matches an expected size exp_size. If it does not match, a runtime error is thrown.

◆ makeObjectiveFunction()

ObjectiveFunction TasOptimization::makeObjectiveFunction ( const int  num_dimensions,
const ObjectiveFunctionSingle  f_single 
)
inline

Creates a TasOptimization::ObjectiveFunction object from a TasOptimization::ObjectiveFunctionSingle object.

Given a TasOptimization::ObjectiveFunctionSingle f_single and the size of its input num_dimensions, returns a TasOptimization::ObjectiveFunction that evaluates a batch of points $ x_1,\ldots,x_k $ to $ {\rm f\_single}(x_1),\ldots, {\rm f\_single}(x_k) $.

◆ computeStationarityResidual()

double TasOptimization::computeStationarityResidual ( const std::vector< double > &  x,
const std::vector< double > &  x0,
const std::vector< double > &  gx,
const std::vector< double > &  gx0,
const double  lambda 
)
inline

Computes the minimization stationarity residual for a point x evaluated from a gradient descent step at x0 with stepsize lambda. More specifically, this residual is an upper bound for the quantity:

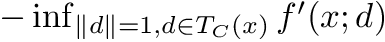
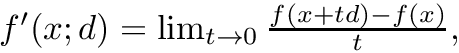
$ -\inf_{\|d\| = 1, d\in T_C(x)} f'(x;d) $ where $ f'(x;d)=\lim_{t \to 0} \frac{ f(x+td)-f(x) }{ t }, $

the set $C$ is the domain of $f$, and $T_C(x)$ is the tangent cone of $C$ at $x$. Here, the gradient of x (resp. x0) is gx (resp. gx0).