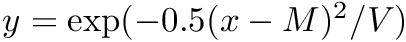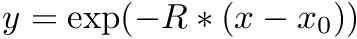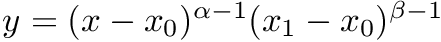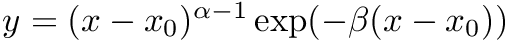Collaboration diagram for Probability distributions, analytic formulas and sampling algorithms:

Functions
void	TasDREAM::applyUniformUpdate (std::vector< double > &x, double magnitude, std::function< double(void)> get_random01=tsgCoreUniform01)
	Add a correction to every entry in x, use uniform samples over (-magnitude, magnitude). More...

void	TasDREAM::applyGaussianUpdate (std::vector< double > &x, double magnitude, std::function< double(void)> get_random01=tsgCoreUniform01)
	Add a correction to every entry in x, sue Gaussian distribution with zero mean and standard deviation equal to magnitude. More...

void	TasDREAM::genUniformSamples (const std::vector< double > &lower, const std::vector< double > &upper, int num_samples, std::vector< double > &x, std::function< double(void)> get_random01=tsgCoreUniform01)
	Generate uniform random samples in the hypercube defined by lower and upper limits. More...

std::vector< double >	TasDREAM::genUniformSamples (const std::vector< double > &lower, const std::vector< double > &upper, int num_samples, std::function< double(void)> get_random01=tsgCoreUniform01)
	Overload that returns the vector.

void	TasDREAM::genGaussianSamples (const std::vector< double > &means, const std::vector< double > &deviations, int num_samples, std::vector< double > &x, std::function< double(void)> get_random01=tsgCoreUniform01)
	Generate standard normal samples with given means and standard deviations. More...

std::vector< double >	TasDREAM::genGaussianSamples (const std::vector< double > &means, const std::vector< double > &deviations, int num_samples, std::function< double(void)> get_random01=tsgCoreUniform01)
	Overload that returns the vector.

template<TypeDistribution distribution, TypeSamplingForm form = regform, typename... Params>
double	TasDREAM::getDensity (double x, Params... params)
	Returns the unscaled probability density of distribution (defined by params) at the point x. More...

Detailed Description

Contains the analytic definitions of several probability distributions and algorithms to draw samples from several known distributions.

Function Documentation

◆ applyUniformUpdate()

void TasDREAM::applyUniformUpdate	(	std::vector< double > &	x,
		double	magnitude,
		std::function< double(void)>	get_random01 = `tsgCoreUniform01`
	)

inline

Add a correction to every entry in x, use uniform samples over (-magnitude, magnitude).

The function get_random01() returns random numbers distributed over (0, 1).

◆ applyGaussianUpdate()

void TasDREAM::applyGaussianUpdate	(	std::vector< double > &	x,
		double	magnitude,
		std::function< double(void)>	get_random01 = `tsgCoreUniform01`
	)

inline

Add a correction to every entry in x, sue Gaussian distribution with zero mean and standard deviation equal to magnitude.

The function get_random01() returns random numbers distributed over (0, 1). Gaussian numbers are generated using the Box-Muller algorithm.

◆ genUniformSamples()

void TasDREAM::genUniformSamples	(	const std::vector< double > &	lower,
		const std::vector< double > &	upper,
		int	num_samples,
		std::vector< double > &	x,
		std::function< double(void)>	get_random01 = `tsgCoreUniform01`
	)

inline

Generate uniform random samples in the hypercube defined by lower and upper limits.

The size of the lower and upper must match. The output vector x will be resized to match num_samples times upper.size(), and the values will be overwritten. The function get_random01() returns random numbers distributed over (0, 1).

◆ genGaussianSamples()

void TasDREAM::genGaussianSamples	(	const std::vector< double > &	means,
		const std::vector< double > &	deviations,
		int	num_samples,
		std::vector< double > &	x,
		std::function< double(void)>	get_random01 = `tsgCoreUniform01`
	)

inline

Generate standard normal samples with given means and standard deviations.

Generate Gaussian (normal) vectors with given means and standard deviations. The means and deviations must have the same size. The function get_random01() returns random numbers distributed over (0, 1).

◆ getDensity()

template<TypeDistribution distribution, TypeSamplingForm form = regform, typename... Params>

double TasDREAM::getDensity	(	double	x,
		Params...	params
	)

Returns the unscaled probability density of distribution (defined by params) at the point x.

Variadric template that defines different one dimensional probability density function. Each function is defined by the distribution type and a set of parameters params, but the densities are not normalized (this is not needed by the DREAM algorithm). Returns the value of the density function at x, but assumes x is in the domain, i.e., if the probability distribution is restricted to an interval no check is performed. For example, for uniform distribution over (a, b), the function will always return 1.

Both the regular and log-form of the density can be computed based on form.

Uniform distribution, dist_uniform,: No additional parameters are needed, always returns 1, e.g.,
double foo = getDensity<dist_uniform>(0.2); // foo will be 1.0

Gaussian distribution, dist_gaussian: Uses two parameters, mean and variance, defined in that order, e.g.,
double y = getDensity<dist_gaussian>(x, M, V);

then $y = \exp(- 0.5 (x - M)^2 / V)$ . Note that this also works for truncated Gaussian distribution, since the range and scale are not considered.

Exponential distribution, dist_exponential: Uses two parameters, lower bound and rate (or inverse scale), e.g.,
double y = getDensity<dist_exponential>(x, x0, R);

then $y = \exp(- R * (x - x_0))$ .

Beta distribution, dist-beta: Uses four parameters, lower and upper bounds and two shapes, e.g.,
double y = getDensity<dist_beta>(x, x0, x1, alpha, beta);

then $y = (x - x_0)^{\alpha - 1} (x_1 - x_0)^{\beta - 1}$ .

Gamma distribution, dist-beta: Uses three parameters, lower bounds, shape and rate, e.g.,
double y = getDensity<dist_gamma>(x, x0, alpha, beta);

then $y = (x - x_0)^{\alpha - 1} \exp(-\beta (x - x_0))$ .

Functions

Detailed Description

Function Documentation

◆ applyUniformUpdate()

◆ applyGaussianUpdate()

◆ genUniformSamples()

◆ genGaussianSamples()

◆ getDensity()