Load from Unstructured Point Set

Collaboration diagram for Load from Unstructured Point Set:

Functions
void	TasGrid::loadUnstructuredDataL2 (double const data_points[], int num_data, double const model_values[], double tolerance, TasmanianSparseGrid &grid)
	Construct a sparse grid surrogate using a least-squares fit. More...
void	TasGrid::loadUnstructuredDataL2 (std::vector< double > const &data_points, std::vector< double > const &model_values, double tolerance, TasmanianSparseGrid &grid)
	Overload that used vectors and infers the number of data points from the size of the vectors. More...

Detailed Description

Templates that infer sparse grid coefficients from a set of unstructured points and model values. These work very similar to TasGrid::loadNeededPoints(), but the data is not assumed to align to the sparse grid. While removing some of the restrictions, the unstructured approach always requires more data to achieve the same level of accuracy compared to the carefully chosen points, and the approximation is valid only in the convex hull of the data, i.e., extrapolating outside of the data-cloud is not mathematically stable. In the interior of the data-cloud, the accuracy of the surrogate is very sensitive to the distribution of the points and good accuracy can be achieved only in areas where the points are sufficiently dense.

The inference usually relies on solving some linear or non-linear problem which may not be stable and may require additional regularization, especially if the data is not sufficient to provide values for all hierarchical coefficients, e.g., all data falls outside of the support of some locally supported basis functions.

Function Documentation

loadUnstructuredDataL2() [1/2]

void TasGrid::loadUnstructuredDataL2 ( double const  data_points[], int  num_data, double const  model_values[], double  tolerance, TasmanianSparseGrid &  grid  )

inline

Construct a sparse grid surrogate using a least-squares fit.

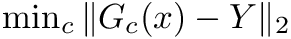
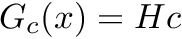
Constructs the coefficients of the grid using a least-squares fit , where c indicates the hierarchical coefficients of the grid, x indicates the data-points and Y is the associated model outputs. The problem is set as a linear system of equations so that where H is the matrix of hierarchical coefficients. Depending on the distribution of the points and/or the type of grid, the system may not be well posed, hence the simple regularization option to add tolerance multiplied by the norm of c.

Parameters

data_points	array of data points similar to TasmanianSparseGrid::loadConstructedPoints() with size grid.getNumDimensions() by num_data
num_data	the number of data points
model_values	array of model values corresponding to the data_points, the size is grid.getNumOutputs() by num_data
tolerance	if positive, will add regularization to the least-squares problem, must be less than the accuracy of the surrogate so that it will not affect the approximation error; if set to zero or less, no regularization will be used but depending on the type of grid and the distribution of the points, the problem may not be well posed
grid	is a non-empty grid, if a refinement has been set, it will be merged with the existing points before inference

Exceptions

std::runtime_error	if the grid is empty or accel_none is used
std::runtime_error	on various cuda errors, e.g., not enough GPU memory, or if the matrix G_c does not have a full column rank, e.g., regularization tolerance is 0 and the data is not sufficient to provide coefficients for all basis functions

The problem requires the QR factorization of G_c and the solution against multiple right hand sides corresponding to the model outputs. This is computationally very expensive and cannot be done without an appropriate acceleration mode:

• accel_cpu_blas will perform all operations on the CPU using OpenMP and the BLAS and LAPACK implementations, OpenMP is optional but recommended
• accel_gpu_cublas will form G_c on the CPU, but then the matrix will be moved to the GPU device and will perform the solver stage using cuBlas and cuSolverDn
• accel_gpu_cuda will form G_c on the GPU and perform the solve using cuBlas and cuSolverDn, if the there is no GPU algorithm for the corresponding TasmanianSparseGrid::evaluateHierarchicalFunctionsGPU() then the CPU will be used identical to the cublas mode
• accel_gpu_magma will form G_c on the GPU device, but will do so in batches as to limit the GPU memory used at a given time, then the linear algebra will be performed using the MAGMA out-of-core methods

The cuda and cublas modes, require that the data and the associated matrices fit in the memory of the GPU device, MAGMA does not have that restriction.

loadUnstructuredDataL2() [2/2]

void TasGrid::loadUnstructuredDataL2 ( std::vector< double > const &  data_points, std::vector< double > const &  model_values, double  tolerance, TasmanianSparseGrid &  grid  )

inline

Overload that used vectors and infers the number of data points from the size of the vectors.

See TasGrid::loadUnstructuredDataL2() for details, in addition

Exceptions

std::runtime_error

if the sizes of the data_points and model_values do not match