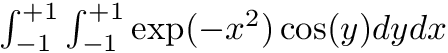Sparse Grids Example 1: integrate a simple function over a canonical domain.
#endif
cout << "\n---------------------------------------------------------------------------------------------------\n";
cout << std::scientific; cout.precision(17);
cout << "Example 1: integrate f(x,y) = exp(-x^2) * cos(y),\n"
<< " using clenshaw-curtis nodes and grid of type level\n";
int dimension = 2;
int level = 6;
std::vector<double> points = grid.
getPoints();
double I = 0.0;
for(int i=0; i<num_points; i++){
double x = points[i*dimension];
double y = points[i*dimension+1];
I += weights[i] * std::exp(-x*x) * std::cos(y);
}
double exact = 2.513723354063905e+00;
double E = std::abs(exact - I);
cout << " at level: " << level
<< "\n the grid has: " << num_points
<< "\n integral: " << I
<< "\n error: " << E << "\n\n";
level = 7;
I = 0.0;
for(int i=0; i<num_points; i++){
double x = points[i*dimension];
double y = points[i*dimension+1];
I += weights[i] * std::exp(-x*x) * std::cos(y);
}
E = std::abs(exact - I);
cout << " at level: " << level
<< "\n the grid has: " << num_points
<< "\n integral: " << I
<< "\n error: " << E << endl;
#ifndef __TASMANIAN_DOXYGEN_SKIP
The master-class that represents an instance of a Tasmanian sparse grid.
Definition TasmanianSparseGrid.hpp:293
int getNumPoints() const
Returns getNumLoaded() if positive, otherwise returns getNumNeeded(), see getPoints().
Definition TasmanianSparseGrid.hpp:661
std::vector< double > getQuadratureWeights() const
Returns a vector of size getNumPoints() of the quadrature weights of the grid.
Definition TasmanianSparseGrid.hpp:747
std::vector< double > getPoints() const
Returns the loaded points if any, otherwise returns the needed points.
Definition TasmanianSparseGrid.hpp:724
void makeGlobalGrid(int dimensions, int outputs, int depth, TypeDepth type, TypeOneDRule rule, std::vector< int > const &anisotropic_weights, double alpha=0.0, double beta=0.0, const char *custom_filename=nullptr, std::vector< int > const &level_limits=std::vector< int >())
Make a Global Grid using Lagrange polynomials with support over the entire domain.
@ rule_clenshawcurtis
Classic nested rule using Chebyshev nodes with very low Lebesgue constant.
Definition tsgEnumerates.hpp:289
@ type_level
Ignoring the polynomial space, use rules with index .
Definition tsgEnumerates.hpp:209