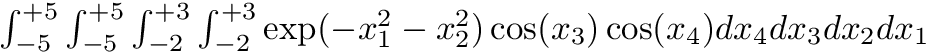Tasmanian Sparse Grids module, example 3

Collaboration diagram for Tasmanian Sparse Grids module, example 3:

Functions
void	sparse_grids_example_03 ()
	Sparse Grids Example 3: compare different quadrature rules. More...

Detailed Description

Example 3

Compute using different rules and precision.

Function Documentation

sparse_grids_example_03()

void sparse_grids_example_03

(

)

Sparse Grids Example 3: compare different quadrature rules.

The example considers a 4D function that is well approximated in a total degree polynomial space. In one and two dimensions, the Gauss-Legendre rule with tensor type gives creates an approximation with the largest total degree space per number of points. In higher dimensions (4 in this case), the sparse (level and qptotal) types have an advantage but the sparse grid construction suffers because the rule is non-nested. The nested Clenshaw-Curtis rule generates about the same total degree space per number of points, but unlike the non-nested rule the extra points are not wasted and hence the approximation is better. The Gauss-Patterson rule, which combines the higher exactness with forced nested structure, outperforms all other methods in precision per number of points.

#endif
 
    cout << "\n---------------------------------------------------------------------------------------------------\n";
    cout << std::scientific; cout.precision(2);
    cout << "Example 3: integrate exp(-x1^2 - x2^2) * cos(x3) * cos(x4)\n"
         << "           for x1, x2 in [-5,5]; x3, x4 in [-2,3];\n"
         << "           using different rules and total degree polynomial space\n\n";
 
    int dimensions = 4;
    double exact = 1.861816427518323e+00 * 1.861816427518323e+00; // exact solution
 
    // creates a grid over the desired domain with specified precision and rule
    auto make_grid = [&](int precision, TasGrid::TypeOneDRule rule)->
        TasGrid::TasmanianSparseGrid{
            auto grid = TasGrid::makeGlobalGrid(dimensions, 0, precision,
                                                TasGrid::type_qptotal, rule);
            grid.setDomainTransform({-5.0, -5.0, -2.0, -2.0}, {5.0, 5.0, 3.0, 3.0});
            return grid;
        };
 
    // computes the integral using the quadrature provided by the grid
    // then prints the number of points and the error
    auto print_error = [&](TasGrid::TasmanianSparseGrid const &grid)->
        void{
            auto points = grid.getPoints();
            auto weights = grid.getQuadratureWeights();
            double integral = 0.0;
            for(size_t i=0; i<weights.size(); i++){
                double x1 = points[4*i + 0];
                double x2 = points[4*i + 1];
                double x3 = points[4*i + 2];
                double x4 = points[4*i + 3];
                integral += weights[i] * std::exp(-x1*x1 - x2*x2) * std::cos(x3) * std::cos(x4);
            }
            cout << setw(10) << grid.getNumPoints() << setw(10) << std::abs(integral - exact);
        };
 
    cout << setw(10) << " " << setw(20) << "Clenshaw-Curtis"
         << setw(20) << "Gauss-Legendre" << setw(20) << "Gauss-Patterson\n";
    cout << setw(10) << "precision" << setw(10) << "points" << setw(10) << "error"
         << setw(10) << "points" << setw(10) << "error"
         << setw(10) << "points" << setw(10) << "error\n";
 
    // print the error for different precision
    for(int precision=5; precision<=40; precision += 5){
        cout << setw(10) << precision;
        print_error( make_grid(precision, TasGrid::rule_clenshawcurtis) );
        print_error( make_grid(precision, TasGrid::rule_gausslegendreodd) );
        print_error( make_grid(precision, TasGrid::rule_gausspatterson) );
        cout << "\n";
    }
 
    cout << "\nAt 311K points the Gauss-Legendre error is O(1.E-1),\n"
         <<   "                   Clenshaw-Curtis error is O(1.E-7) at 320K points.\n";
    cout << "At 70K points the Gauss-Patterson error is O(1.E-4),\n"
         << "                  Clenshaw-Curtis needs 158K points to achieve the same." << endl;
 
#ifndef __TASMANIAN_DOXYGEN_SKIP