Collaboration diagram for Enumerated types:

Enumerations
enum	TasGrid::TypeIndexRelation { TasGrid::type_abeforeb , TasGrid::type_bbeforea , TasGrid::type_asameb }
	Describes the relation between two multi-indexes when compared during sorting. More...

enum	TasGrid::TypeDepth { TasGrid::type_none , TasGrid::type_level , TasGrid::type_curved , TasGrid::type_hyperbolic , TasGrid::type_iptotal , TasGrid::type_qptotal , TasGrid::type_ipcurved , TasGrid::type_qpcurved , TasGrid::type_iphyperbolic , TasGrid::type_qphyperbolic , TasGrid::type_tensor , TasGrid::type_iptensor , TasGrid::type_qptensor }
	Used by Global Sequence and Fourier grids, indicates the selection criteria. More...

enum	TasGrid::TypeOneDRule { TasGrid::rule_none , TasGrid::rule_clenshawcurtis , TasGrid::rule_clenshawcurtis0 , TasGrid::rule_fejer2 , TasGrid::rule_chebyshev , TasGrid::rule_chebyshevodd , TasGrid::rule_leja , TasGrid::rule_lejaodd , TasGrid::rule_rleja , TasGrid::rule_rlejadouble2 , TasGrid::rule_rlejadouble4 , TasGrid::rule_rlejaodd , TasGrid::rule_rlejashifted , TasGrid::rule_rlejashiftedeven , TasGrid::rule_rlejashifteddouble , TasGrid::rule_maxlebesgue , TasGrid::rule_maxlebesgueodd , TasGrid::rule_minlebesgue , TasGrid::rule_minlebesgueodd , TasGrid::rule_mindelta , TasGrid::rule_mindeltaodd , TasGrid::rule_gausslegendre , TasGrid::rule_gausslegendreodd , TasGrid::rule_gausspatterson , TasGrid::rule_gausschebyshev1 , TasGrid::rule_gausschebyshev1odd , TasGrid::rule_gausschebyshev2 , TasGrid::rule_gausschebyshev2odd , TasGrid::rule_gaussgegenbauer , TasGrid::rule_gaussgegenbauerodd , TasGrid::rule_gaussjacobi , TasGrid::rule_gaussjacobiodd , TasGrid::rule_gausslaguerre , TasGrid::rule_gausslaguerreodd , TasGrid::rule_gausshermite , TasGrid::rule_gausshermiteodd , TasGrid::rule_customtabulated , TasGrid::rule_localp , TasGrid::rule_localp0 , TasGrid::rule_semilocalp , TasGrid::rule_localpb , TasGrid::rule_wavelet , TasGrid::rule_fourier }
	Used to specify the one dimensional family of rules that induces the sparse grid. More...

enum	TasGrid::TypeRefinement { TasGrid::refine_classic , TasGrid::refine_parents_first , TasGrid::refine_direction_selective , TasGrid::refine_fds , TasGrid::refine_stable , TasGrid::refine_none }
	Refinement strategy for local polynomial and wavelet grids. More...

enum	TasGrid::TypeAcceleration { TasGrid::accel_none , TasGrid::accel_cpu_blas , TasGrid::accel_gpu_default , TasGrid::accel_gpu_cublas , TasGrid::accel_gpu_cuda , TasGrid::accel_gpu_magma }
	Modes of acceleration. More...

Variables
constexpr TypeAcceleration	TasGrid::accel_gpu_hip = accel_gpu_cuda
	At the front API, the HIP and CUDA options are equivalent, see TasGrid::TypeAcceleration.

constexpr TypeAcceleration	TasGrid::accel_gpu_rocblas = accel_gpu_cublas
	At the front API, the HIP and CUDA options are equivalent, see TasGrid::TypeAcceleration.

Detailed Description

Enumerated types: Enumerations are used as input to many Tasmanian functions in both internal and external API.

Enumeration Type Documentation

◆ TypeIndexRelation

enum TasGrid::TypeIndexRelation

Describes the relation between two multi-indexes when compared during sorting.

The standard C++11 algorithms std::merge and std::binary_search use bools as return types when comparing entries, thus in the case of many repeated entries, two comparisons have to be performed. Repeated entries are encountered in many sparse grids algorithms, especially when dealing with nested one dimensional rules. Thus, for performance reasons, Tasmanian implements merging and searching methods that compare multi-indexes and produce three outcomes in a single comparison.

Specifically, see SetManipulations::push_merge_map() and MultiIndexSet::getSlot() and MultiIndexSet::addSortedInsexes()

Enumerator
type_abeforeb	Indicates that the first multi-index in the call to compare comes before the second.
type_bbeforea	Indicates that the second multi-index in the call to compare after the second.
type_asameb	Indicates that the two multi-indexes are the same.

◆ TypeDepth

enum TasGrid::TypeDepth

Used by Global Sequence and Fourier grids, indicates the selection criteria.

Approximation Error: The approximation error when interpolating or integrating a target model with a Global sparse grid, is bound by a constant multiplied by the best approximation of the model in the set of polynomial exactness. The exactness set consists of all polynomials that can be captured exactly (approximated to round-off error) by the sparse grid. The constant is the norm of the sparse grid operator (a.k.a., the Lebesgue constant) and the exactness set is the range.

: The operator norm depends primarily on the underlying one dimensional rule used to construct the grid, and all rules implemented in Tasmanian have reasonable norms. Of primary focus is the target model and constructing a grid with range suitable for either integrating or interpolating the model.

Categories

The types of Global grids fall into four categories:

Level selection uses the order of the one dimensional rules as criteria and pays no regard to the polynomial exactness. Level types are strongly influenced by the growth of points in the one dimensional rule and are seldom optimal, although such grid can be a good initial guess for an iterative refinement process.
Total degree polynomial space is good for smooth models, i.e., analytic functions with convergent Taylor series for every point in the domain.
Curved polynomial space is essentially a Total degree space with an added logarithmic correction term. The correction can account for rules with slightly higher norm growth (e.g., R-Leja rules) or for models with heavily constrained region of analytic extension, i.e., slightly less smooth.
Hyperbolic cross section space is suitable for models with more irregular behavior, e.g., models with only a finite number of derivatives.

: The four main types can be tuned for either interpolation or quadrature (integration); the corresponding enumerate will have either i or q in the name. In all cases, Tasmanian will construct the grid with minimum number of points (or fewest basis functions), that will capture the corresponding polynomial space.

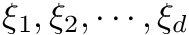
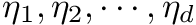
Anisotropic Weights: All types can be combined with anisotropic weights that adjust the density of the grid in different directions. Below, we denote the anisotropic weights with $\xi_1, \xi_2, \cdots, \xi_d$ and $\eta_1, \eta_2, \cdots, \eta_d$ , where is the number of dimensions in the grid. Note that only curved types use the $\eta$ weights.

: The TypeDepth also uses the depth parameter to define a cut-off point, the depth is normalized by multiplying it by the smallest of the $\xi$ weights. In the formulas below, L stands for the normalized offset.

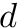
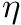
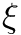
Details regarding sparse grids construction and polynomial spaces can be found in
M. Stoyanov, C. G. Webster, A Dynamically Adaptive Sparse Grid Method for Quasi-Optimal Interpolation of Multidimensional Analytic Functions, arXiv:1508.01125.
also published in Computers and Mathematics with Applications 71 (2016) 2449–2465.

Full Tensor Types: Finally, in addition to the aforementioned types, Tasmanian includes the types for dense tensor grids. Only in 2-dimensions Gauss quadrature rules with full tensors are more efficient than a general sparse grid. Performing interpolation or working with more than 2 dimensions, sparse grids will always result in better approximation error per number of nodes, i.e., model evaluations; nevertheless, dense tensor grids naturally fall in the framework and can be useful for testing purposes.

Fourier Grids: The Fourier grids are very similar to Global grids, with the exception that polynomial powers are replaced by frequencies of trigonometric functions. The different selection strategies can be used with frequency exactness in place of polynomial power.

The structure of the Fourier spaces, the convergence estimates, and the refinement strategies are described in
Z. Morrow, M. Stoyanov, A Method for Dimensionally Adaptive Sparse Trigonometric Interpolation of Periodic Functions, arXiv:1908.10672.

Enumerator
type_none	Null type, should never be used for input, indicates an error of some sort.
type_level	Ignoring the polynomial space, use rules with index $\left\{ (i_1, i_2, \cdots, i_d) : \sum_{k=1}^d \xi_k i_k \leq L \right\}$ .
type_curved	Ignoring the polynomial space, use rules with index $\left\{ (i_1, i_2, \cdots, i_d) : \sum_{k=1}^d \xi_k i_k + \sum_{k=1}^d \eta_k \log(i_k + 1) \leq L \right\}$ .
type_hyperbolic	Ignoring the polynomial space, use rules with index $\left\{ (i_1, i_2, \cdots, i_d) : \prod_{k=1}^d (i_k + 1)^{\xi_k} \leq L \right\}$ .
type_iptotal	Total degree polynomial space for interpolation, i.e., the span of $\left\{ \prod_{k=1}^d x^{i_k} : \sum_{k=1}^d \xi_k i_k \leq L \right\}$ .
type_qptotal	Total degree polynomial space for quadrature/integration.
type_ipcurved	Curved polynomial space for interpolation, i.e., the span of $\left\{ \prod_{k=1}^d x^{i_k} : \sum_{k=1}^d \xi_k i_k + \sum_{k=1}^d \eta_k \log(i_k + 1) \leq L \right\}$ .
type_qpcurved	Curved polynomial space for quadrature/integration.
type_iphyperbolic	Hyperbolic cross section polynomial space for interpolation, i.e., the span of $\left\{ \prod_{k=1}^d x^{i_k} : \prod_{k=1}^d (i_k + 1)^{\xi_k} \leq L \right\}$ .
type_qphyperbolic	Hyperbolic cross section polynomial space for quadrature/integration.
type_tensor	Make a dense tensor grid with rules indexed by $\xi_1, \xi_2, \cdots, \xi_d$ .
type_iptensor	Make a dense tensor grid with interpolation range that includes $\left\{ \prod_{k=1}^d x^{i_k} : i_k \leq \xi_k \mbox{ for all } k \right\}$ .
type_qptensor	Make a dense tensor grid with quadrature/integration range that includes $\left\{ \prod_{k=1}^d x^{i_k} : i_k \leq \xi_k \mbox{ for all } k \right\}$ .

◆ TypeOneDRule

enum TasGrid::TypeOneDRule

Used to specify the one dimensional family of rules that induces the sparse grid.

One Dimensional Rules: A sparse grid is a superposition of tensors of one dimensional rules with varying precision in the different directions. In this context, a TypeOneDRule defines a family of one dimensional rules with corresponding abscissas (nodes), quadrature weights, and basis functions.

Categories

The rules fall into 5 categories, corresponding to the 5 main classes of grids.

Global using Lagrange polynomials for interpolation and (sometimes) specialized quadrature weights.
Sequence rules are a subset of the Global rules, Sequence rules are always nested and each level adds one node to the previous level.
Local Polynomial rules use uniformly spaced nodes and polynomial basis with localized support.
Wavelet and Fourier rules also use uniformly spaced nodes, but with wavelet and trigonometric basis functions.

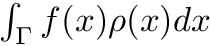
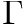
Special Quadrature: All rules can be used to approximate integrals of the form $\int_\Gamma f(x) \rho(x) dx$ where $\Gamma$ is the (transformed) domain and is the model. The majority of rules assume that the weight is constant 1, but in some cases more exotic weights are used. Assume that constant weight 1 is used, unless otherwise specified.

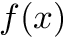
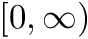
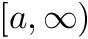
Domain Transformation: Most rules are defined on a canonical interval [-1, 1], which can be transformed to an arbitrary [a, b] with TasmanianSparseGrid::setDomainTransform(), so long as a is less than b. Fourier grids use canonical [0, 1] and can be similarly transformed to [a, b]. Gauss-Laguerre rule is set to $[0, \infty)$ transformed to $[a, \infty)$ with scale parameter b (see below). 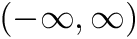Gauss-Hermite is set to $(-\infty, \infty)$ with scale and shift parameters.

Enumerator
rule_none	Null rule, should never be used as input (default rule for an empty grid).
rule_clenshawcurtis	Classic nested rule using Chebyshev nodes with very low Lebesgue constant.
rule_clenshawcurtis0	Same as rule_clenshawcurtis but with modified basis that assumes the model is zero at the boundary.
rule_fejer2	Similar to rule_clenshawcurtis but with nodes strictly in the interior.
rule_chebyshev	Using Chebyshev nodes with very low Lebesgue constant and slow node growth, but non-nested.
rule_chebyshevodd	Same as rule_chebyshev but using only odd levels, partially mitigates the non-nested issues.
rule_leja	Classic sequence rule, moderate Lebesgue constant growth (empirical result only).
rule_lejaodd	Same as rule_leja but using only odd levels, quadrature is more stable.
rule_rleja	Classic sequence rule based on complex analysis, moderate Lebesgue constant growth (theoretically proven).
rule_rlejadouble2	Using rule_rleja nodes but doubling the nodes every 2 levels, reduces the Lebesgue constant.
rule_rlejadouble4	Using rule_rleja nodes but doubling the nodes every 4 levels, reduces the Lebesgue constant.
rule_rlejaodd	Same as rule_rleja but using only odd levels, quadrature is more stable.
rule_rlejashifted	Similar sequence to rule_rleja but with nodes strictly in the interior.
rule_rlejashiftedeven	Same as rule_rlejashifted but using only even levels, quadrature is more stable.
rule_rlejashifteddouble	Same as rule_rlejashifted but doubling the number of nodes per level, which reduced the Lebesgue constant.
rule_maxlebesgue	A greedy sequence rule with nodes placed at the maximum of the Lebesgue function.
rule_maxlebesgueodd	Same as rule_maxlebesgue but using only odd levels, quadrature is more stable.
rule_minlebesgue	A greedy sequence rule with nodes added to minimize the Lebesgue constant.
rule_minlebesgueodd	Same as rule_minlebesgue but using only odd levels, quadrature is more stable.
rule_mindelta	A greedy sequence rule with nodes added to minimize the norm of the surplus operator.
rule_mindeltaodd	Same as rule_mindelta but using only odd levels, quadrature is more stable.
rule_gausslegendre	Non-nested rule but optimized for integration.
rule_gausslegendreodd	Same as rule_gausslegendre but using only odd levels, partially mitigates the non-nested issues.
rule_gausspatterson	Nested rule that is optimized for integration, probably the best integration rule in more than 2 dimensions.
rule_gausschebyshev1	Non-nested rule optimized for integral of the form $\int_{a}^{b} f(x) / \sqrt{(b - x)(x - a)} dx$ .
rule_gausschebyshev1odd	Same as rule_gausschebyshev1 but using only odd levels, partially mitigates the non-nested issues.
rule_gausschebyshev2	Non-nested rule optimized for integral of the form $\int_{a}^{b} f(x) \sqrt{(b - x)(x - a)} dx$ .
rule_gausschebyshev2odd	Same as rule_gausschebyshev2 but using only odd levels, partially mitigates the non-nested issues.
rule_gaussgegenbauer	Non-nested rule optimized for integral of the form $\int_{a}^{b} f(x) (b - x)^\alpha (x - a)^\alpha dx$ .
rule_gaussgegenbauerodd	Same as rule_gaussgegenbauer but using only odd levels, partially mitigates the non-nested issues.
rule_gaussjacobi	Non-nested rule optimized for integral of the form $\int_{a}^{b} f(x) (b - x)^\alpha (x - a)^\beta dx$ .
rule_gaussjacobiodd	Same as rule_gaussjacobi but using only odd levels, partially mitigates the non-nested issues.
rule_gausslaguerre	Non-nested rule optimized for integral of the form $\int_{a}^{\infty} f(x) (x - a)^\alpha \exp \left(-b (x - a) \right) dx$ .
rule_gausslaguerreodd	Same as rule_gausslaguerre but using only odd levels, partially mitigates the non-nested issues.
rule_gausshermite	Non-nested rule optimized for integral of the form $\int_{-\infty}^{\infty} f(x) (x - a)^\alpha \exp \left(-b (x - a)^2 \right) dx$ .
rule_gausshermiteodd	Same as rule_gausshermite but using only odd levels, partially mitigates the non-nested issues.
rule_customtabulated	User provided rule, nodes and weights must be provided with a separate file.
rule_localp	Nested rule with a hierarchy of uniformly distributed nodes and functions with compact support.
rule_localp0	Variation of rule_localp assuming the model is zero at the domain boundary.
rule_semilocalp	Variation of rule_localp using increased support in exchange for higher order basis (better for smoother functions).
rule_localpb	Variation of rule_localp focusing nodes on the boundary instead of the interior.
rule_wavelet	Wavelet basis with uniformly distributed nodes (primarily for internal use).
rule_fourier	Trigonometric basis with uniformly distributed nodes (primarily for internal use).

◆ TypeRefinement

enum TasGrid::TypeRefinement

Refinement strategy for local polynomial and wavelet grids.

Local Hierarchical Approximation: The nodes and basis functions used in local polynomial and wavelet sparse grid form a complex multidimensional hierarchy, where each node is associated with one or more parents and children in each direction. In both cases, the support of the children is (almost always) smaller than the support of the patent and in the polynomial case, the support of the children nodes is strictly contained within the support of the parent.

: The interpolant is expressed as a linear combination of basis functions with coefficients computed so that the interpolant matches the model values at the sparse gird nodes. The coefficients are thus indicators of the local approximation error and (in the asymptotic limit) the coefficients decrease when going form a parent to a child.

Convergence Criteria: Using the local error estimator, the sparse grid approximation has reached desired tolerance when all nodes with missing children have coefficients with absolute values smaller than the tolerance. This is a necessary and not a sufficient condition an is heavily reliant on the assumption of monotonic decay of the coefficients; however, in practical situations this is a good way to construct an adaptive grid that captures the behavior of the target model while minimizing the number of nodes.

Adaptive Refinement: The idea of refinement is to start with a coarse spars grid and gradually add children of existing nodes, but only if the nodes have a large hierarchical coefficient. The nodes are added until the coefficients of all nodes with with missing children drop below user specified tolerance. The refinement types listed below differ in the way that the parents and children are selected in the adaptive construction, and whether local anisotropy is considered.

Refinement Types: Each nodes is associated with multiple parents corresponding to different directions, even if each one dimensional node has only a single parent. Thus, over several iterations and if the hierarchical coefficients do not decay monotonically, it is possible to have nodes with missing parents for some directions, which can hinter convergence. Furthermore, the hierarchical coefficients do not carry any information regarding potential local anisotropy and a second refinement criteria can be employed, where an interpolant is constructed using only the data associated with the nodes that lay in a single direction. Children and/or parents of a node are added to the grid only when both the isotropic and anisotropic error indicators exceed the user specified tolerance.

: The classic refinement strategy adds only the children for the nodes with hierarchical coefficient that exceed the user provided tolerance (local anisotropy and missing parents are ignored). The parents first and fds strategies loop for missing parents and add the parents before adding children, which usually improves stability when compared to adding only children. The direction selective and fds strategies consider local anisotropy which can reduce the number of required model evaluations, but can also lead to decrease in stability. The stable refinement is both isotropic and maintains lower-complete structures, i.e., no point has a missing parent. While the most stable, the stable strategy can lead to significant oversampling.

Details regarding adaptive hierarchical sparse grids construction and children-parent relations can be found in:
M. Stoyanov, Adaptive Sparse Grid Construction in a Context of Local Anisotropy and Multiple Hierarchical Parents,
Sparse Grids and Applications - Miami 2016 pp 175-199.
Also in: Tech Report ORNL/TM-2013/384.

Enumerator
refine_classic	Isotropic refinement using only the children and disregarding missing parents.
refine_parents_first	Isotropic refinement adding children only if the parents are already included.
refine_direction_selective	Anisotropic refinement using only the children and disregarding missing parents.
refine_fds	Anisotropic refinement adding children only if the parents are already included.
refine_stable	Isotropic refinement that ensures the points maintain lower-complete structures.
refine_none	Null method, should never be used as input.

◆ TypeAcceleration

enum TasGrid::TypeAcceleration

Modes of acceleration.

Acceleration Context: Each Tasmanian object creates a Tasmanian acceleration context that operate on one of several modes (depending on the external libraries being used) and the context will remain persistent on read/write, make/clean, and move operation. The context cannot be copied from one object to another. For example, an object is created and CUDA acceleration is enabled, then makeLocalPolynomial() is called, then the Nvidia GPU device will be used to speed the different operation of the grid, if then read() is called, a new grid will be loaded from a file and regardless of the type of grid the GPU will still be in use by the object. If the grid is copied, both source and destination will retain their original acceleration contexts and only the grid data (e.g., points and model values) will be copied.

Utilizing Accelerated Libraries: Each Tasmanian operation that has a (potentially) significant computational cost is a candidate for acceleration. Currently, OpenMP is uses throughout the Tasmanian code is essentially all potential places and the evaluateBatch() methods associated with all types of grids can be accelerated with BLAS and CUDA. The BLAS/LAPACK and CUDA acceleration is also available in other select methods, e.g., TasmanianSparseGrid::loadNeededPoints() for local polynomial and wavelet grid.

OpenMP and Thread Count: If enabled, OpenMP is ubiquitous throughout Tasmanian in almost all computationally expensive operations. The acceleration mode can be disabled only at compile time; however, the standard OpenMP options are respected at runtime, e.g., the method omp_set_num_threads() and OMP_NUM_THREADS environment variable, if either is set to 1, Tasmanian will use only one hardware thread.

Acceleration Mode None: In this mode, Tasmanian will forego the use of third party libraries (other then OpenMP) and the algorithms will run in the most memory conservative way. Due to improved data-locality and depending on the hardware architecture, the TasGrid::accel_none mode can be the fastest mode for small grids with few points and few outputs.

Memory Management and Persistent Data: The use of third party libraries requires that matrices are explicitly formed even when that can be avoided in the no-acceleration mode. Furthermore, operations that are called repeatedly, i.e., evaluateBatch() used in the context of DREAM sampling, will also cache matrices that can be reused in multiple calls. The cache is particularly an issue for the various GPU modes since the memory on the accelerator devices is sometimes limited. One-shot calls, such as loadNeededPoints(), will not use cache that persistent after the call to the method. The cache can always be cleared by either changing the grid (creating a new grid or loading more points as part of iterative refinement), or by switching to mode TasGrid::accel_none and then back to one of the fast modes.

Memory usage for Evaluate Batch: Global, Sequence, Fourier and Wavelet grids operate only with dense matrices and require one persistent matrix of size getNumPoints() times getNumOutputs(), one temporary matrix of size getNumPoints() times num_x, and user provided matrix to hold the result of size getNumOutputs() times num_x. The batch size num_x can be adjusted to accommodate memory constraints, but better performance is usually achieved when num_x is large due to the increased opportunities to parallelize. Local polynomial grids (when using the default sparse mode) will use sparse representation of the transient matrix and thus the memory usage strongly depends on the graph structure of the grid. In addition, all grids use a relatively small amount of GPU cache which depends on the number of underlying tensors and the specific graph structure of the grid.

Defaults

If Tasmanian_ENABLE_BLAS is enabled in CMake, then TasGrid::accel_cpu_blas will be the default acceleration mode, otherwise the default mode is TasGrid::accel_none. The TasGrid::accel_gpu_default uses the first available in the list:

: The defaults and fallback extend to all methods that could use accelerations. For example, if GPU acceleration has been enabled, but the current method does not have a GPU implementation, the "next-best" BLAS implementation will be used instead. Thus, the use of BLAS and LAPACK can be disabled either at compile time or with accel_none, but not with accel_gpu_cuda.

: Note that regardless of the acceleration mode, all evaluate methods will to generate output that is identical up to rounding error. By design, the TasmanianSparseGrid::enableAcceleration() can be called with any acceleration type regardless whether it has been enabled by CMake. In order to facilitate code portability, Tasmanian implements sane fall-back modes so that "the next best mode" will be automatically selected if the desired mode is not present. Specifically, missing MAGMA will fallback to CUDA, missing CUDA will fallback to BLAS, and missing BLAS will fallback to none.

Thread Safety and Const-correctness: Using mode TasGrid::accel_none, Tasmanian will not use any transient data-structures and the code is const-correct in the strictest definition, i.e., any two const-methods can be called concurrently from any two threads and will produce the correct result. Other modes use transient cache (with the C++ keyword mutable), which will be generated after the first call to the method and will be reused in follow on call. Thus, the first call is not thread-safe, while the follow on calls are strictly const-correct in the same sense as TasGrid::accel_none. Also note that some third party libraries can have additional restrictions, e.g., concurrent calls to OpenBLAS are not thread-safe unless the library is build with a specific flag. The CUDA and MAGMA libraries appear to not have such limitations.

Library Handles

The GPU libraries use context handles to manage metadata such as active device and device pointer type. By default, Tasmanian will automatically create the handles whenever needed and will destroy them whenever the object is destroyed or the acceleration mode is updated. However, Tasmanian also provides an API where the user can provide the corresponding handles:

// Nvidia CUDA framework
grid.setCuBlasHandle(cublas_handle);
grid.setCuSparseHandle(cusparse_handle);
grid.setCuSolverHandle(cusolverdn_handle);
// AMD ROCm framework
grid.setRocBlasHandle(rocblas_handle);
grid.setRocSparseHandle(rocsparse_handle);
// Intel DPC++ framework
grid.setSycleQueue(pointer_to_sycl_queue);

Each handle must be a valid, i.e., already created by the corresponding API call and must be associated with the currently selected GPU device ID.
Tasmanian assumes that the pointer mode is "host pointer" (for Nvidia and AMD) and if a different mode is set in-between Tasmanian API calls, the mode must be reset before the next Tasmanian call.
The SYCL queue is accepted as a pointer, which is different then the usual SYCL approach but it is consistent within the Tasmanian API.
The methods interact directly with the TPL API and hence the methods do not have fallback modes if GPU has not been enabled.

Enumerator
accel_none	Usually the slowest mode, uses only OpenMP multi-threading, but optimized for memory and could be the fastest mode for small problems.
accel_cpu_blas	Default (if available), uses both BLAS and LAPACK libraries.
accel_gpu_default	Equivalent to the first available from MAGMA, CUDA, BLAS, or none.
accel_gpu_cublas	Mixed usage of the CPU (OpenMP) and GPU libraries.
accel_gpu_cuda	Similar to the cuBLAS option but also uses a set of Tasmanian custom GPU kernels.
accel_gpu_magma	Same the CUDA option but uses the UTK MAGMA library for the linear algebra operations.

Enumerations

Variables