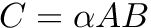TasGrid::TasGpu Namespace Reference

Wrappers around custom CUDA kernels to handle domain transforms and basis evaluations, the kernels are instantiated in tsgCudaKernels.cu. More...

Functions
template<typename scalar_type >
void	solveLSmultiGPU (AccelerationContext const *acceleration, int n, int m, scalar_type A[], int nrhs, scalar_type B[])
	Least squares solver with data sitting on the gpu device.
template<typename scalar_type >
void	solveLSmultiOOC (AccelerationContext const *acceleration, int n, int m, scalar_type A[], int nrhs, scalar_type B[])
	Identical to TasGpu::solveLSmultiGPU() but the arrays are on the CPU and the MAGMA out-of-core implementation is used.
template<typename scalar_type >
void	solveLSmulti (AccelerationContext const *acceleration, int n, int m, scalar_type A[], int nrhs, scalar_type B[])
	Identical to TasGpu::solveLSmultiGPU() but the data starts with the CPU and gets uploaded to the GPU first.
void	factorizePLU (AccelerationContext const *acceleration, int n, double A[], int_gpu_lapack ipiv[])
	Factorize , arrays are on the GPU.
void	solvePLU (AccelerationContext const *acceleration, char trans, int n, double const A[], int_gpu_lapack const ipiv[], double b[])
	Solve A x = b using a PLU factorization.
void	solvePLU (AccelerationContext const *acceleration, char trans, int n, double const A[], int_gpu_lapack const ipiv[], int nrhs, double B[])
	Solve A x = b using a PLU factorization, B is in row-major format.
template<typename scalar_type >
void	denseMultiply (AccelerationContext const *acceleration, int M, int N, int K, typename GpuVector< scalar_type >::value_type alpha, GpuVector< scalar_type > const &A, GpuVector< scalar_type > const &B, typename GpuVector< scalar_type >::value_type beta, scalar_type C[])
	Wrapper to GPU BLAS that multiplies dense matrices (e.g., cuBlas, MAGMA).
template<typename scalar_type >
void	denseMultiplyMixed (AccelerationContext const *acceleration, int M, int N, int K, typename GpuVector< scalar_type >::value_type alpha, GpuVector< scalar_type > const &A, scalar_type const B[], typename GpuVector< scalar_type >::value_type beta, scalar_type C[])
	Identical to TasGpu::denseMultiply() but both B and C are array in CPU memory.
template<typename scalar_type >
void	sparseMultiply (AccelerationContext const *acceleration, int M, int N, int K, typename GpuVector< scalar_type >::value_type alpha, const GpuVector< scalar_type > &A, const GpuVector< int > &pntr, const GpuVector< int > &indx, const GpuVector< scalar_type > &vals, scalar_type C[])
	Wrapper to GPU methods that multiplies a sparse and a dense matrix.
template<typename T >
void	sparseMultiplyMixed (AccelerationContext const *acceleration, int M, int N, int K, typename GpuVector< T >::value_type alpha, const GpuVector< T > &A, const std::vector< int > &pntr, const std::vector< int > &indx, const std::vector< T > &vals, T C[])
	Identical to TasGpu::sparseMultiply() but the sparse matrix and the result C are in CPU memory.

Detailed Description

Wrappers around custom CUDA kernels to handle domain transforms and basis evaluations, the kernels are instantiated in tsgCudaKernels.cu.

Function Documentation

solveLSmultiGPU()

template<typename scalar_type >

void TasGrid::TasGpu::solveLSmultiGPU	(	AccelerationContext const *	acceleration,
		int	n,
		int	m,
		scalar_type	A[],
		int	nrhs,
		scalar_type	B[]
	)

Least squares solver with data sitting on the gpu device.

Solves the least squares problem 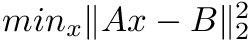where A has n rows and m columns (n >= m) and B has n rows and nrhs columns. Both matrices are stored in row-major format on the GPU device associated with the given acceleration. The matrix B will be overwritten with the solution.

denseMultiply()

template<typename scalar_type >

void TasGrid::TasGpu::denseMultiply	(	AccelerationContext const *	acceleration,
		int	M,
		int	N,
		int	K,
		typename GpuVector< scalar_type >::value_type	alpha,
		GpuVector< scalar_type > const &	A,
		GpuVector< scalar_type > const &	B,
		typename GpuVector< scalar_type >::value_type	beta,
		scalar_type	C[]
	)

Wrapper to GPU BLAS that multiplies dense matrices (e.g., cuBlas, MAGMA).

Computes 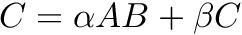where A is M by K, B is K by N, and C is M by N all stored in column major format on the GPU device associated with the acceleration. The signature is near identical to BLAS sgemm() or dgemm() but there are no transpose variants and the leading dimensions are inferred as if the matrices have no padding.

sparseMultiply()

template<typename scalar_type >

void TasGrid::TasGpu::sparseMultiply	(	AccelerationContext const *	acceleration,
		int	M,
		int	N,
		int	K,
		typename GpuVector< scalar_type >::value_type	alpha,
		const GpuVector< scalar_type > &	A,
		const GpuVector< int > &	pntr,
		const GpuVector< int > &	indx,
		const GpuVector< scalar_type > &	vals,
		scalar_type	C[]
	)

Wrapper to GPU methods that multiplies a sparse and a dense matrix.

Computes where A is M by K, B is K by N, and C is M by N, matrices are in column major format with B being sparse in column compressed format.