tsgCoreOneDimensional.hpp File Reference

Algorithms and meta-data for the Gauuss, Chebyshev and custom rules. More...

#include "tsgIOHelpers.hpp"
#include "tsgLinearSolvers.hpp"
#include "tsgSequenceOptimizer.hpp"

Include dependency graph for tsgCoreOneDimensional.hpp:

This graph shows which files directly or indirectly include this file:

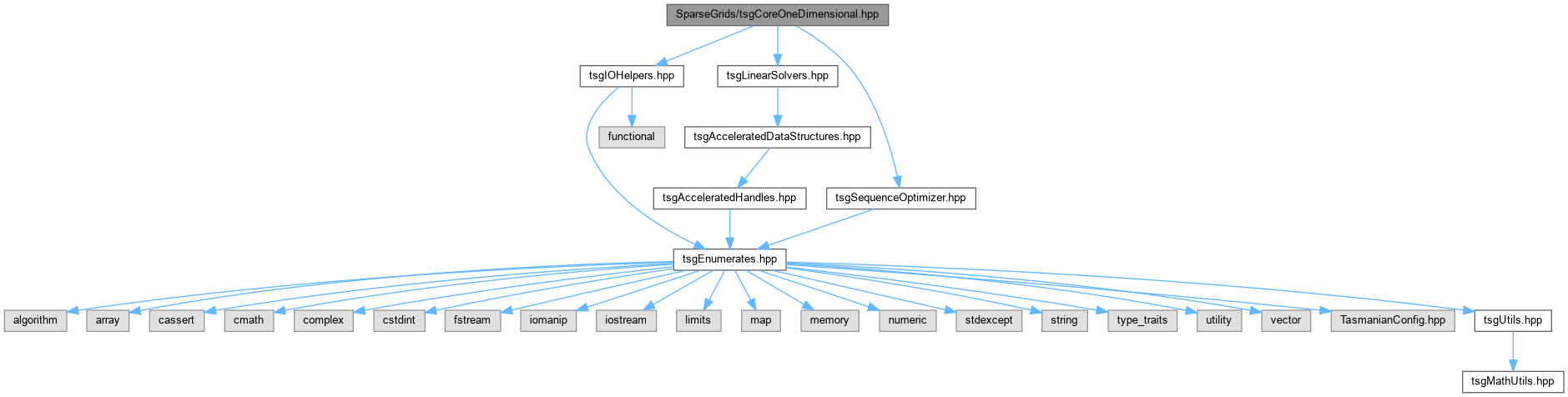
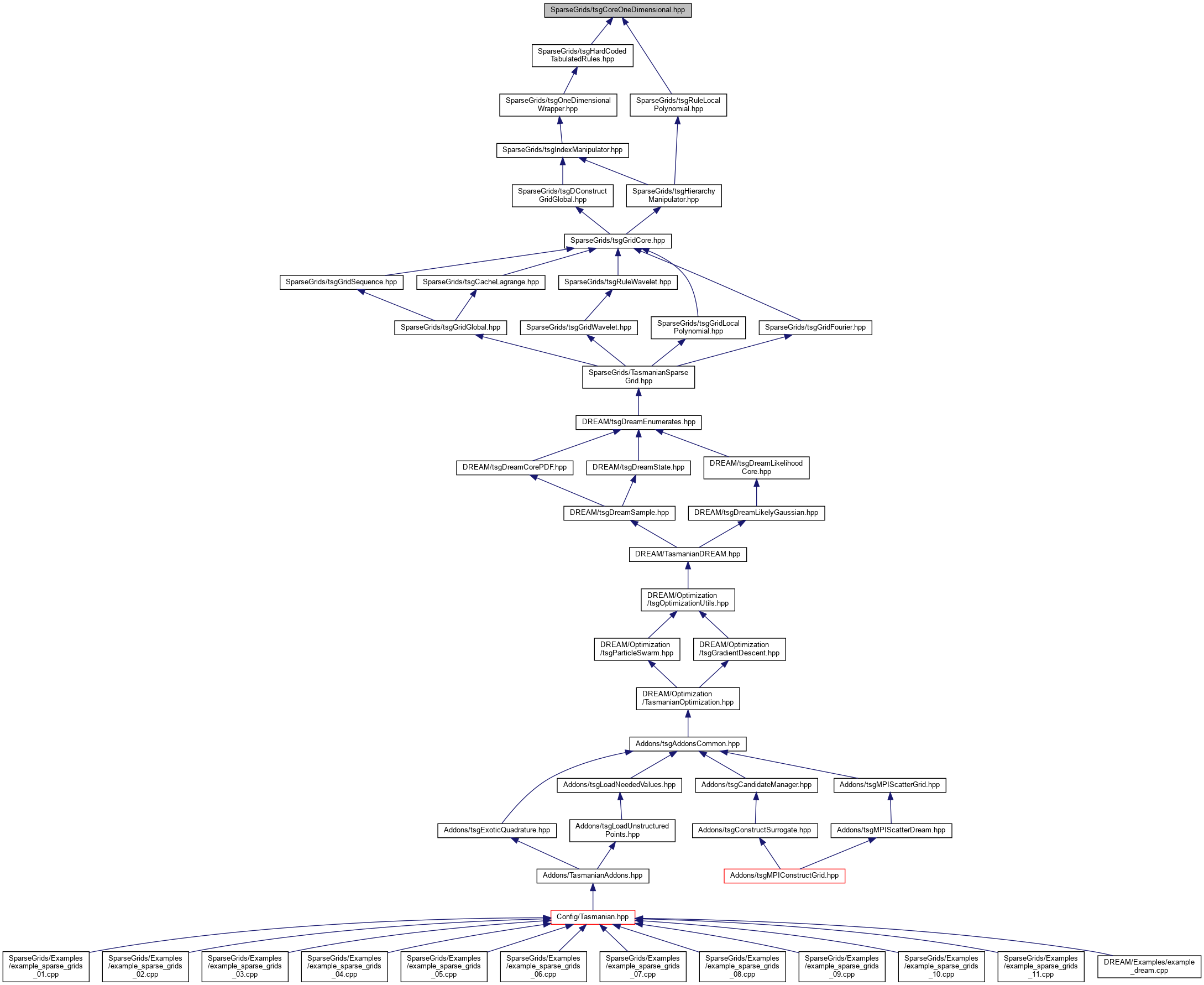
Go to the source code of this file.

Classes
class	TasGrid::CustomTabulated
	Class providing manipulation of custom tabulated rules, file I/O and structured access to the points, weights, and meta-data. More...

Namespaces
namespace	TasGrid
	Encapsulates the Tasmanian Sparse Grid module.
namespace	TasGrid::OneDimensionalMeta
	Metadata for one dimensional rules, number of points, exactness, I/O, etc.
namespace	TasGrid::OneDimensionalNodes
	Contains algorithms for generating Gauss,Chebyshev, and Fourier nodes and weights.

Functions
CustomTabulated	TasGrid::getSubrules (CustomTabulated &ct, int start_index, int stride, std::string description)
	Generates a subset of rules as a CustomTabulated object. The subset has a short description string given by description and takes the levels of the input ct starting from level start_index with distance stride between consecutive levels.

Detailed Description

Algorithms and meta-data for the Gauuss, Chebyshev and custom rules.

Author

Miroslav Stoyanov

Contains core information about one dimensional rules, custom tabulated, Chebyshev and Gaussian rules. Also, generic I/O data.