Linear solvers

Collaboration diagram for Linear solvers:

Files
file	tsgLinearSolvers.hpp
	Linear solvers.

Namespaces
namespace	TasGrid::TasmanianDenseSolver
	Methods for dense linear algebra.
namespace	TasGrid::TasmanianTridiagonalSolver
	Methods for tridiagonal eigenvalue problems.
namespace	TasGrid::TasmanianFourierTransform
	Methods for Fast-Fourier-Transform.
namespace	TasGrid::TasSparse
	Methods for sparse linear algebra.

Classes
class	TasGrid::TasSparse::WaveletBasisMatrix
	Used to manipulate the wavelet values and solve for the wavelet coefficients. More...

Functions
void	TasGrid::TasmanianDenseSolver::solveLeastSquares (int n, int m, const double A[], double b[], double *x)
	Least squares solver, used to infer anisotropic coefficients and thus rarely exceeds 10 - 20.
void	TasGrid::TasmanianFourierTransform::fast_fourier_transform (std::vector< std::vector< std::complex< double > > > &data, std::vector< int > &num_points)
	Transfrom the data for a multi-dimensional tensor.
void	TasGrid::TasmanianFourierTransform::fast_fourier_transform1D (std::vector< std::vector< std::complex< double > > > &data, std::vector< int > &indexes)
	Perform one dimensional fast-fourier-transform (using radix-3).

Detailed Description

Linear Solvers

Many sparse grids methods rely on various linear solvers, sparse iterative, eigenvalue, fast-fourier-transform, and least-squares. Some solvers use third-party-libraries, e.g., BLAS and LAPACK, but others are implemented specifically for Tasmanian. The custom solvers are tuned for the specific problems and can (in the specific circumstances) outperform than general third-party methods. Thus, balance is maintained between external dependencies, performance, and capabilities.

Function Documentation

solveLeastSquares()

void TasGrid::TasmanianDenseSolver::solveLeastSquares	(	int	n,
		int	m,
		const double	A[],
		double	b[],
		double *	x
	)

Least squares solver, used to infer anisotropic coefficients and thus rarely exceeds 10 - 20.

Solves 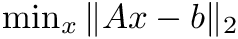where A is an n by m matrix (column major format), and b and x are vectors with sizes n and m. The assumption here is that n is larger than m (the problem is over-determined) and A has full column rank. The use case is for the rates of anisotropic decay which never exceed twice the number of dimensions and are hence not too large and expensive.

fast_fourier_transform()

void TasGrid::TasmanianFourierTransform::fast_fourier_transform	(	std::vector< std::vector< std::complex< double > > > &	data,
		std::vector< int > &	num_points
	)

Transfrom the data for a multi-dimensional tensor.

The num_points vector defines the number of points used by the tensor in different directions. The data holds the values for each point in the tensor, each point has a vector of values with size equal to the number of model outputs.

The data is split into one-dimensional lines and each is tackled with fast_fourier_transform1D()

fast_fourier_transform1D()

void TasGrid::TasmanianFourierTransform::fast_fourier_transform1D	(	std::vector< std::vector< std::complex< double > > > &	data,
		std::vector< int > &	indexes
	)

Perform one dimensional fast-fourier-transform (using radix-3).

Consider the line which is a subset of data defined by indexes and perform the radix-3 fast-fourier-transform. Called from fast_fourier_transform().