tsgLinearSolvers.hpp File Reference

Linear solvers. More...

#include "tsgAcceleratedDataStructures.hpp"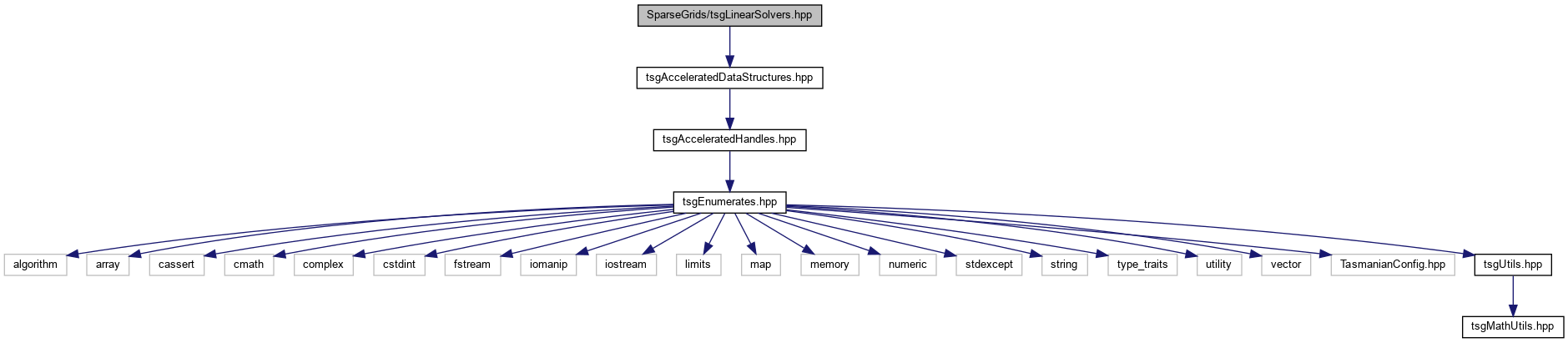

Include dependency graph for tsgLinearSolvers.hpp:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Classes
class	TasGrid::TasSparse::WaveletBasisMatrix
	Used to manipulate the wavelet values and solve for the wavelet coefficients. More...

Namespaces
	TasGrid
	Encapsulates the Tasmanian Sparse Grid module.
	TasGrid::TasmanianDenseSolver
	Methods for dense linear algebra.
	TasGrid::TasmanianTridiagonalSolver
	Methods for tridiagonal eigenvalue problems.
	TasGrid::TasmanianFourierTransform
	Methods for Fast-Fourier-Transform.
	TasGrid::TasSparse
	Methods for sparse linear algebra.

Functions
void	TasGrid::TasmanianDenseSolver::solveLeastSquares (int n, int m, const double A[], double b[], double *x)
	Least squares solver, used to infer anisotropic coefficients and thus rarely exceeds 10 - 20. More...
void	TasGrid::TasmanianDenseSolver::solveLeastSquares (AccelerationContext const *acceleration, int n, int m, double A[], double b[], double *x)
	The same solver, but uses LAPACK dgels method (if enabled).
template<typename scalar_type >
void	TasGrid::TasmanianDenseSolver::solvesLeastSquares (AccelerationContext const *acceleration, int n, int m, scalar_type A[], int nrhs, scalar_type B[])
	Least squares solver, operates on multiple right-hand sides and row-major matrices. More...
template<typename scalar_type >
void	TasGrid::TasmanianDenseSolver::solvesLeastSquaresGPU (AccelerationContext const *acceleration, int n, int m, scalar_type A[], int nrhs, scalar_type B[])
	Overload that accepts arrays on the GPU device.
std::vector< double >	TasGrid::TasmanianTridiagonalSolver::getSymmetricEigenvalues (int n, std::vector< double > const &diag, std::vector< double > const &offdiag)
	Method for computing the eigenvalues of a symmetric matrix in place, using an LAPACK wrapper.
void	TasGrid::TasmanianTridiagonalSolver::decompose (std::vector< double > &diag, std::vector< double > &off_diag, const double mu0, std::vector< double > &nodes, std::vector< double > &weights)
	Method for tridiagonal eigenvalue decomposition, used to compute nodes and weights for Gaussian rules. On return, it destroys the inputs diag and offdiag and writes the outputs to nodes and weights. The parameter mu0 should be set to where is the measure in the function inner product. The parameter version specifies which algorithm should be called.
void	TasGrid::TasmanianTridiagonalSolver::decompose1 (int n, std::vector< double > &d, std::vector< double > &e, std::vector< double > &z)
	(decompose_version == 1) TASMANIAN's first internal implementation.
void	TasGrid::TasmanianTridiagonalSolver::decompose2 (std::vector< double > &diag, std::vector< double > &off_diag, const double mu0, std::vector< double > &nodes, std::vector< double > &weights)
	(decompose_version == 2) Based on the ALGOL code for Golub's 1967 report "Calculation of Gauss Quadrature Rules".
void	TasGrid::TasmanianFourierTransform::fast_fourier_transform (std::vector< std::vector< std::complex< double >>> &data, std::vector< int > &num_points)
	Transfrom the data for a multi-dimensional tensor. More...
void	TasGrid::TasmanianFourierTransform::fast_fourier_transform1D (std::vector< std::vector< std::complex< double >>> &data, std::vector< int > &indexes)
	Perform one dimensional fast-fourier-transform (using radix-3). More...

Detailed Description

Linear solvers.

Author

Miroslav Stoyanov

Many sparse grids methods rely on various linear solvers, sparse iterative, eigenvalue, fast-fourier-transform, and least-squares. The solvers are tuned for the specific problems and can perform as good (or even better) than general third-party methods. In addition, this reduces the external dependencies.