Components#
Reno models are based primarily on stocks and flows. A model is created by defining all of these components and the corresponding equations that make them up.
The equations themselves and how to construct them are discussed in more depth on the Math in Reno page, while this page primarily focuses on the higher level Flow/Stock/Variable components.
Flows#
Flows are equations that define rates of change, or represent how much material/information moves over time.
Flows are created with the reno.Flow class, and the equation can either be
directly provided in the constructor or by setting the .eq attribute later
on:
from reno import Flow, TimeRef
import reno
# create a flow with an equation of "5"
faucet = Flow(5) # 5 units per timestep
# change the equation to vary sinusoidally with time
t = TimeRef() # a TimeRef instance is a special type of variable that
# always refers to the current timestep in the simulation
faucet.eq = reno.sin(t) * 2 + 5
Stocks#
A stock represents an accumulation of material or information, or some quantity thereof over time.
Stock equations are defined exclusively in terms of flows, in-flows (rates of material moving into the stock) and out-flows (rates of material moving out of the stock.)
Creating stocks in Reno are done via the Stock class:
from reno import Stock
tub_water_level = Stock()
Defining stock equations#
Stock equations are defined by setting up in-flows and out-flows. The basic
syntax for doing this uses the += operator for in-flows and -= operator for
outflows:
from reno import Stock, Flow
my_inflow, my_outflow = Flow(), Flow()
my_stock = Stock()
my_stock += my_inflow
my_stock -= my_outflow
A slightly more readable syntax that allows constructing whole “chains” of
in-flow/out-flows can be done with the >> and << operators, where the
arrows indicate the direction of a flow in relation to the stock on the other
side:
from reno import Stock, Flow
inflow, midflow, outflow = Flow(), Flow(), Flow()
stock1, stock2 = Stock(), Stock()
inflow >> stock1 >> midflow >> stock2 >> outflow
Specifically a stock >> flow or flow << stock makes flow an
out-flow of stock, and stock << flow or flow >> stock makes
flow an in-flow to stock.
Chains of these >>/<< operations work because they are
interpreted left to right, and the “return” value of an individual operation
is always the right-most component, e.g. component2 in component1 >>
component2.
As a result,
inflow >> stock1 >> midflow
is equivalent to:
inflow >> stock1
stock1 >> midflow
Implicit stock in-flows#
When an in-flow to a stock is set (either through += or >>/<<)
with an equation rather than just a flow, an implicit flow defined by that
equation is created and applied.
(e.g. if there’s some loss involved between the outflow of one stock and the inflow for another, you could of course explicitly model this with two separate flows as well)
from reno import Stock, Flow
inflow, midflow, outflow = Flow(), Flow(), Flow()
stock1, stock2 = Stock(), Stock()
inflow >> stock1 >> midflow
(midflow - 3) >> stock2 >> outflow
by combining operations together on the same line with commas, you can still do a full chain-like definition when an inflow needs to be a slightly modified version:
from reno import Stock, Flow
inflow, midflow, outflow = Flow(), Flow(), Flow()
stock1, stock2 = Stock(), Stock()
inflow >> stock1 >> midflow, (midflow - 3) >> stock2 >> outflow
Using stocks in other equations#
(This might need to have its own section at the end to discuss the difference between circular references involving stocks and those between flows)
Referencing a stock always refers to the stock’s value in the previous timestep. This allows a form of circular reference between stocks
from reno import Stock, Flow
my_flow = Flow()
my_stock = Stock()
my_stock += my_flow
my_flow.eq = 10 - my_stock
In this example, my_stock is incremented by the value of my_flow
in the current timestep t, while the value of my_flow for timestep t
is 10 minus the value of my_stock in timestep t - 1.
In other words, the equations for these would translate to:
my_stock(t) = my_stock(t-1) + my_flow(t)
my_flow(t) = 10 - my_stock(t-1)
Variables#
A variable is any other equation or value that can be referenced in flow (and other variable) equations and helps define the user-settable model parameters. Variables should be used to specify what can be modified about a simulation/what values you want to experiment with.
coffee_process = reno.Model(steps=10)
with coffee_process:
drip_speed = reno.Variable(3.0)
water = reno.Stock(init=100.0)
coffee = reno.Stock()
coffee_machine = reno.Flow(drip_speed, max=water)
water >> coffee_machine >> coffee
In the above model, drip_speed is a variable that directly impacts the
coffee_machine flow/the rate at which coffee increases. Since it is a
free variable/not defined in terms of any other variables, it can be specified
during a model run to configure the simulation. We can run a couple simulations
and compare the final coffee stock values (at timestep 10):
>>> coffee_process(drip_speed=4.0).coffee.values[0, -1]
36.0
>>> coffee_process(drip_speed=1.0).coffee.values[0, -1]
9.0
Metrics#
Metrics are a special type of component whose equations run once, after all the
timesteps of the simulation have been calculated. These equations are normally
used to retrieve a specific value or run a basic analysis/measurement on
something. Metrics are useful from a convenience standpoint (making it
semantically simpler to get e.g. the last value of the coffee stock like in
the previous example), since they are then available to include in Reno’s
Visuzliations, but they can also be used as targets for observed/measured
values (“data”) for Bayesian Inference.
We can add a metric to the previous system to capture the final value in the stock with:
coffee_process.final_coffee_level = reno.Metric(coffee.timeseries[-1])
This would, for example, allow plotting this final value distribution if an
input distribution were specified for drip_speed:
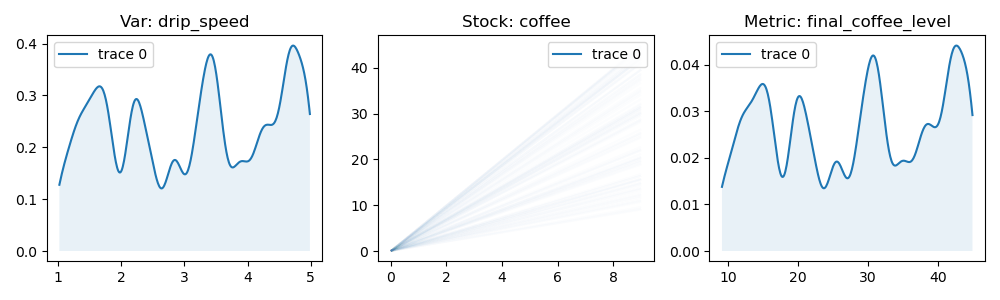
>>> run = coffee_process(n=100, drip_speed=reno.Uniform(1.0, 5.0))
>>> reno.plot_trace_refs(
coffee_process,
[run],
[
coffee_process.drip_speed,
coffee_process.coffee,
coffee_process.final_coffee_level
],
rows=1,
cols=3,
figsize=(10, 3)
)
Other arguments for components#
min/max#
All stock/flow/variable components take several additional optional arguments.
Equation minimum/maximum limits can be defined with equations/values via min
and max. This can be useful to specify on outflows to avoid sending a stock into
negative values (e.g. if it represents a physical quantity.) In the coffee
example above, the coffee_machine flow is initialized with a max=water,
meaning that despite the result of the equation itself, the value won’t be
higher than the water stock in each timestep.
It is important to note that setting a min/max on a stock does not modify inflow values to that stock. To highlight this, the system below defines two stocks with a flow in between:
m = reno.Model()
with m:
s1 = reno.Stock(init=100)
s2 = reno.Stock(max=10)
f1 = reno.Flow(20, max=s1)
s1 >> f1 >> s2
s2 isn’t allowed to contain more than 10, but the inflow is pulling in 20 at
each timestep. Running this model for a few steps, we observe that s2 never goes
above 10, but s1 still decreases by 20 each time, resulting in “dropped” material.
>>> run = m(steps=3)
>>> run.s1.values[0]
array([100, 80, 60])
>>> run.f1.values[0]
array([20, 20, 20])
>>> run.s2.values[0]
array([0, 10, 10])
To appropriately bottleneck a stock like this entails also applying limits to the flow, possibly using something like the space operation discussed on the Math in Reno page.
dim/dtype#
Specifying the dtype (where you pass a regular python type such as float,
int, bool, etc.) of a component ensures the type of the underlying value and
will automatically convert as needed. This type assignment occurs on initial
value population - this either occurs automatically at the beginning of a
simulation, or you have to call populate() yourself:
>>> a = r.Variable(5, dtype=float)
>>> a.eval()
5
>>> a.populate(1, 1)
>>> a.eval()
5.0
Type information is automatically determined/broadcast when not explicitly specified, and converted appropriately when it is:
>>> m = r.Model()
>>> m.a = r.Variable(5)
>>> m.b = r.Variable(m.a)
>>> m.a.dtype, m.b.dtype
(int, int)
>>> m = r.Model()
>>> m.a = r.Variable(5, dtype=float)
>>> m.b = r.Variable(m.a)
>>> m.a.dtype, m.b.dtype
(float, float)
>>> m = r.Model()
>>> m.a = r.Variable(5, dtype=float)
>>> m.b = r.Variable(m.a, dtype=int)
>>> m.a.dtype, m.b.dtype
(float, int)
dim refers to an optional extra “data dimension” which allows you to work
with vector data. Operations automatically broadcast according to numpy rules
(TODO: link broadcasting):
>>> a = r.Variable(5, dim=4)
>>> a.eval()
array([5, 5, 5, 5])
Note that manually specifying dim only applies if the value is not already
vectorized:
>>> a = r.Variable([5, 2], dim=4)
>>> a.eval()
array([5, 2])
cgroup/group#
cgroup and group parameters are used for controlling diagram rendering,
see TODO: link to visualization cgroups page